
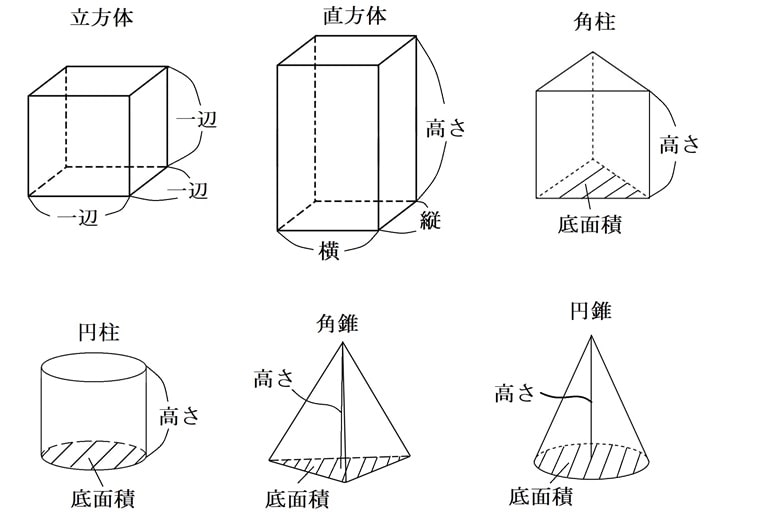
角柱 円柱の体積の公式 小学生に教えるための分かりやすい解説 数学fun
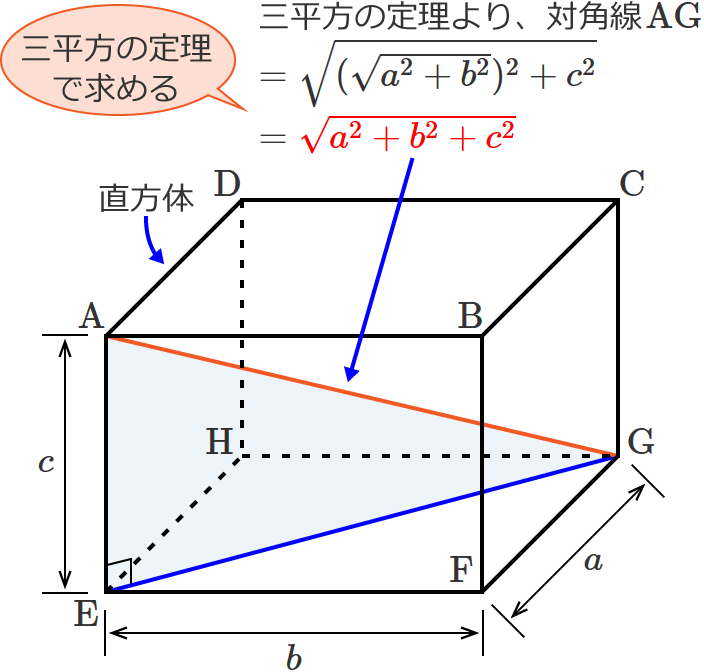
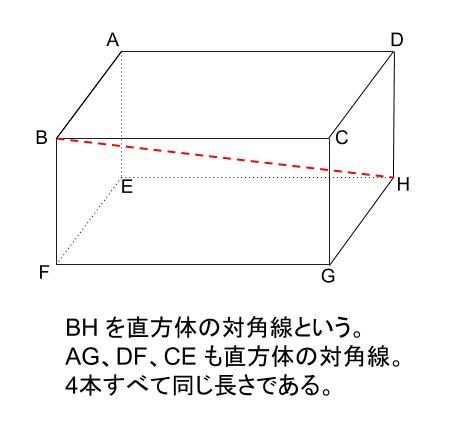
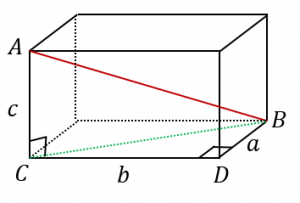
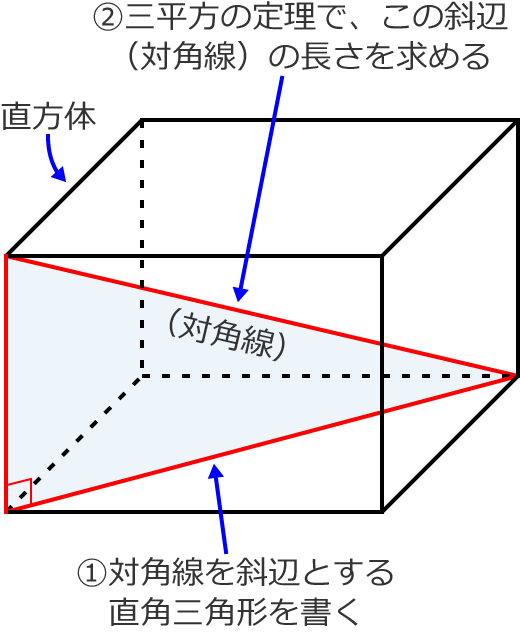
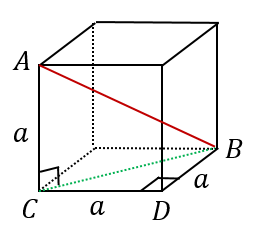
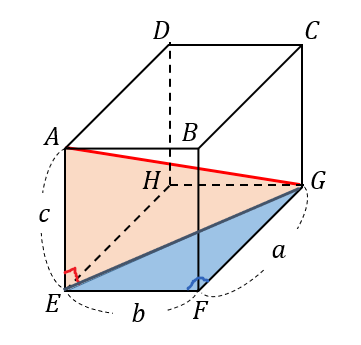
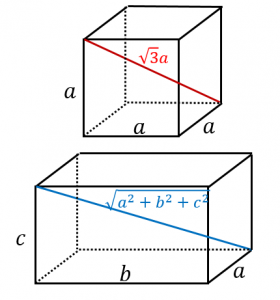
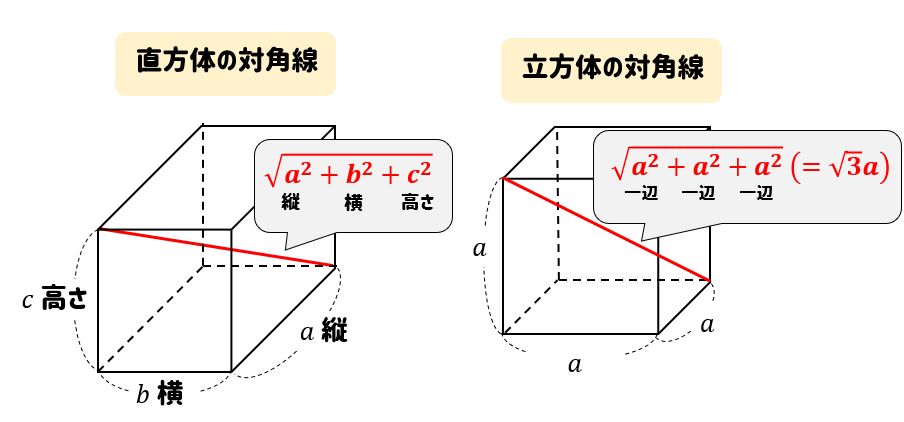
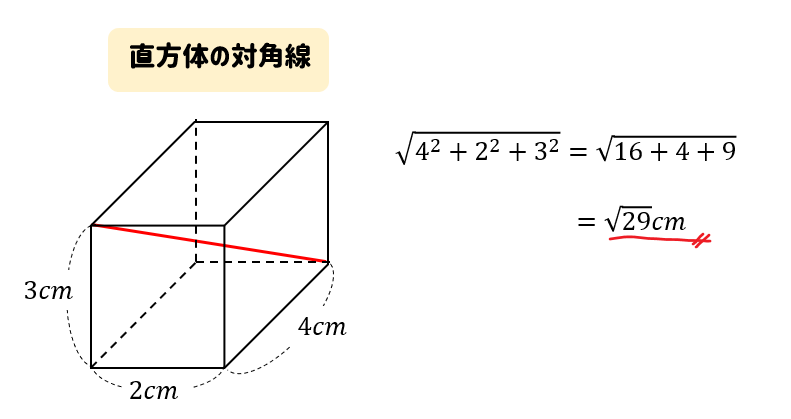
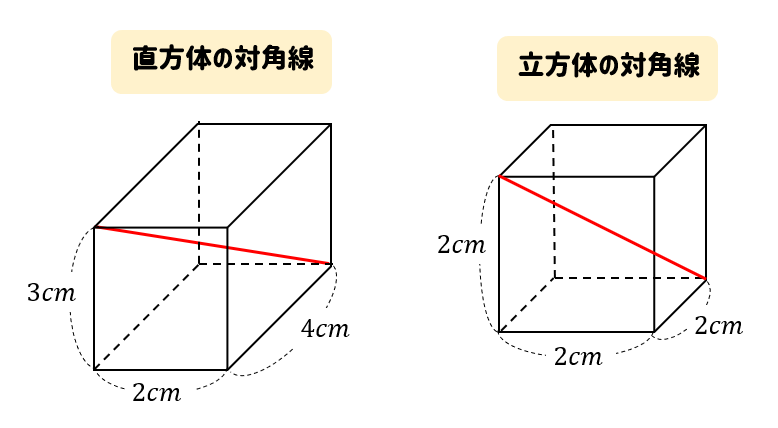
直方体の対角線の長さたて、横、高さがそれぞれ、\(a,b,c\) である直方体の対角線の長さを \(L\) とすると、\(L=\sqrt{a^2b^2c^2}\)三平方の定理の斜辺の長さと似ていますね。「三平方の定理の立体版」って感じがしますね。なぜこの公式なのか直方体の対角線の もともとの三角柱の高さ=三角柱の体積÷底面積=504÷(12×7÷2)=12(cm) 求める三角柱の高さは、もともとの三角柱の高さの3分の1であることから 求める三角柱の高さ=12(cm)÷3=4(cm)となります。 答え 4cm ~立体の体積・表面積を求める公式まとめ
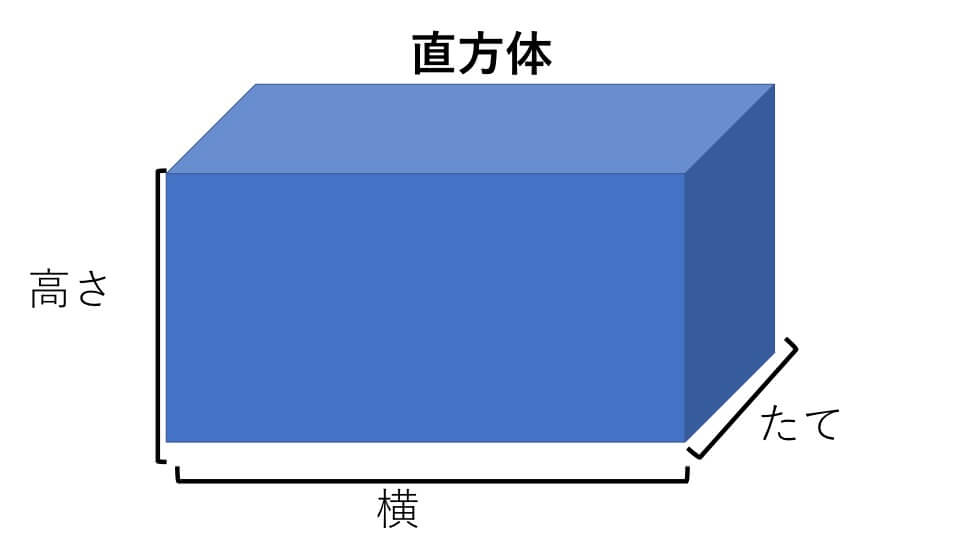
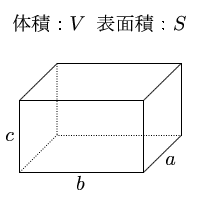
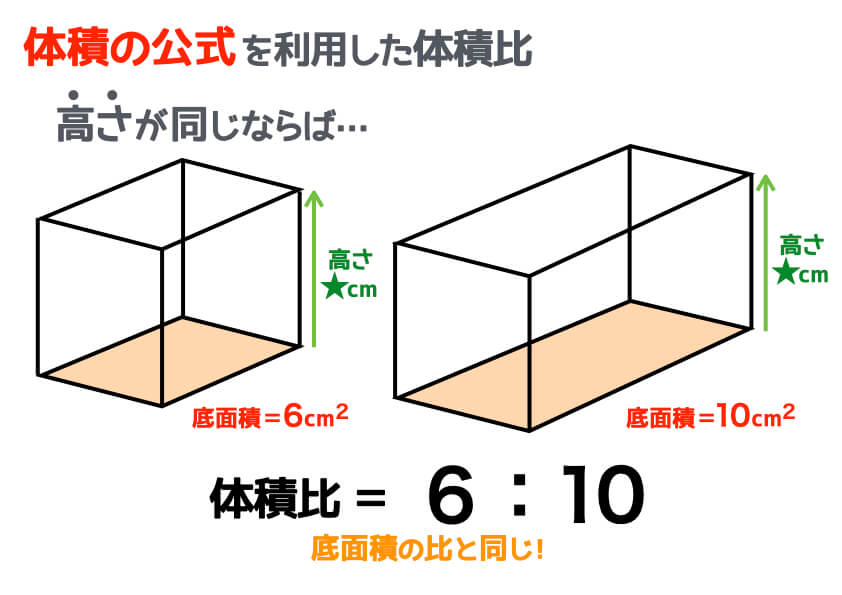
直方体の公式
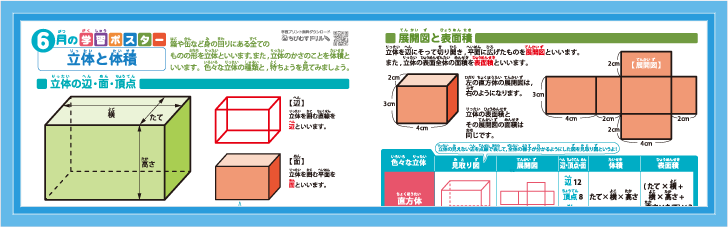
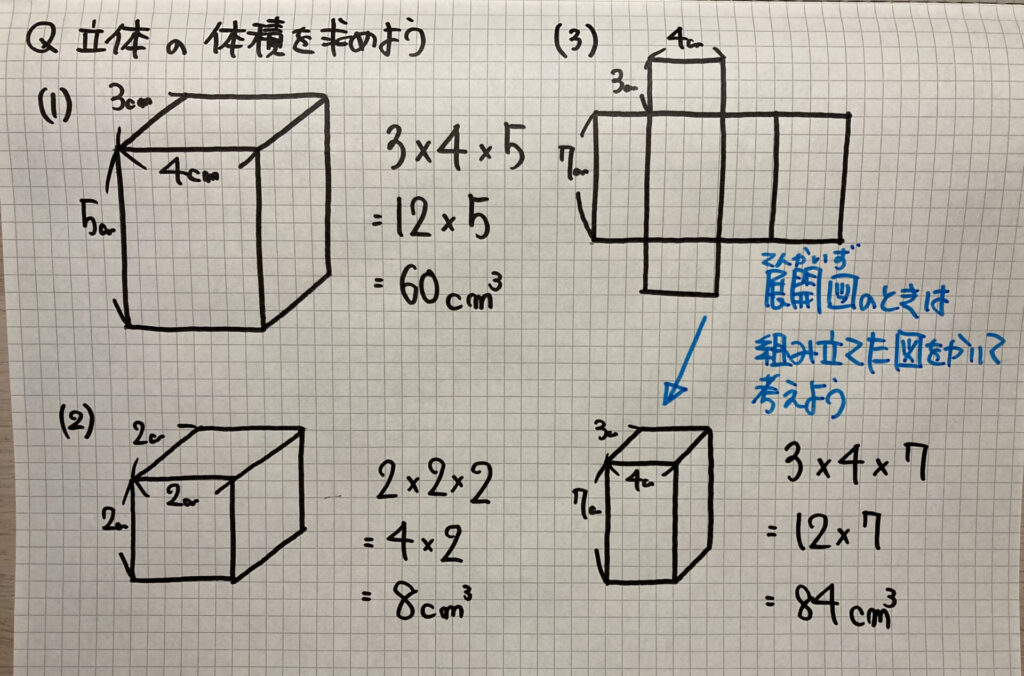
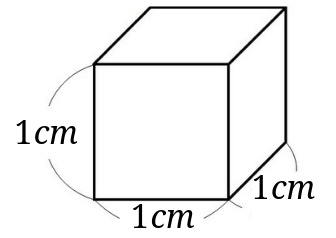
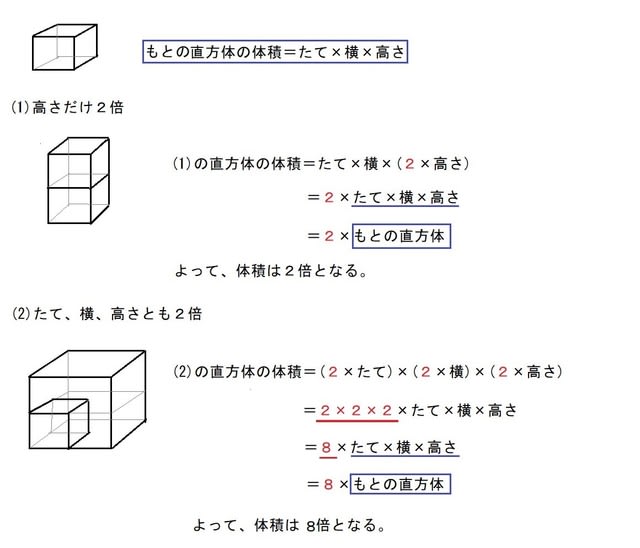
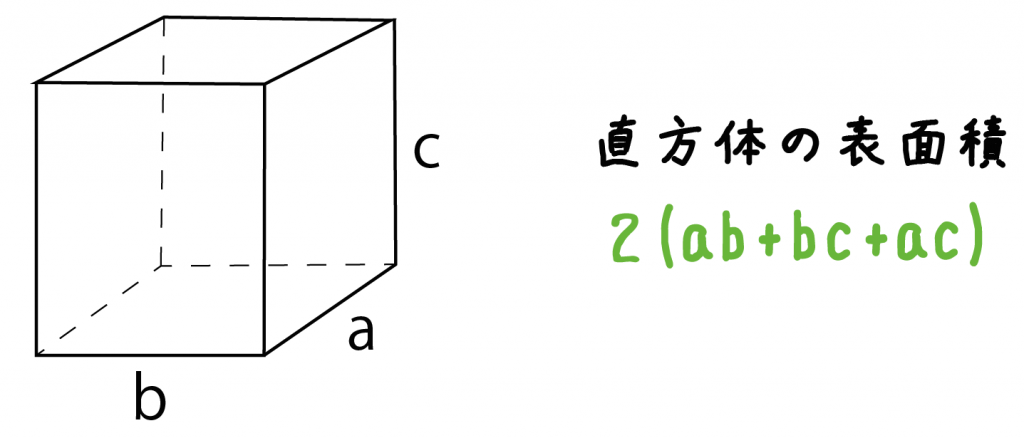
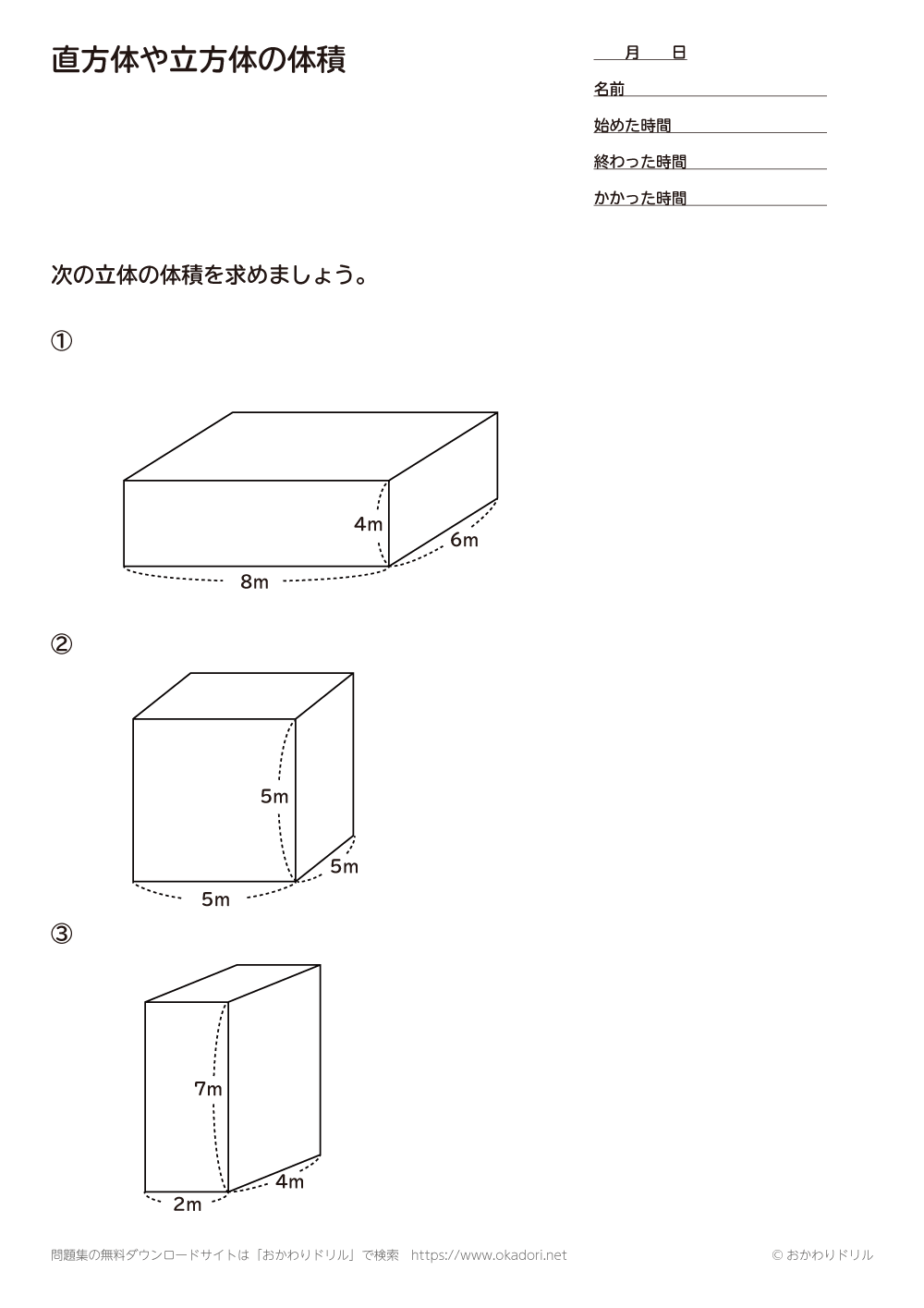
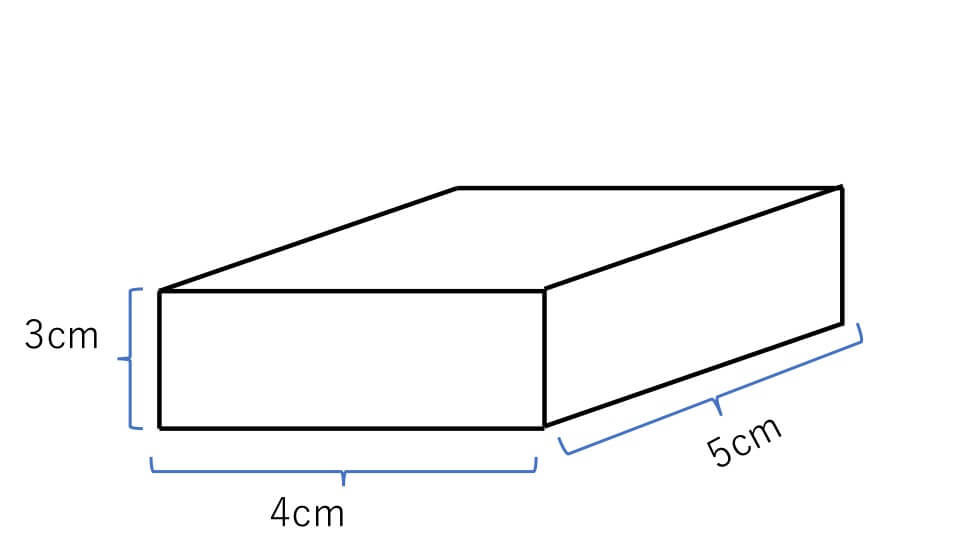
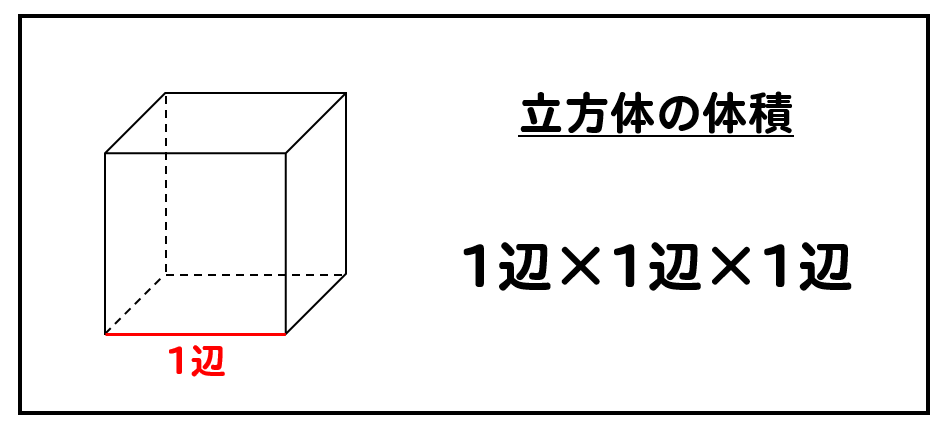
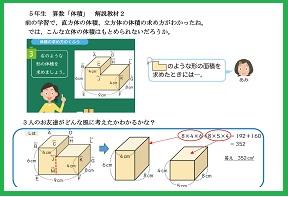
直方体の公式- 体積を求めよう ⑴直方体の体積は公式通りで求めることができますね ⑵立方体は、たて、横、高さが同じになるので 立方体の体積=1辺×1辺×1辺 と別の公式で表すことができます ⑶展開図で図形が書いてある場合は それを組み立てた図を書いて たて慣性モーメントの導出:直方体 21年1月12日 下の図のような質量m、それぞれの辺の長さがa , b , lの直方体の慣性モーメントを求めます 密度をρとすると $$\rho = \frac {m} {abl}$$ 積分範囲は $$\frac {b} {2}\leq x \leq\frac {b} {2} ~~~ \frac {a} {2}\leq y \leq\frac {a} {2
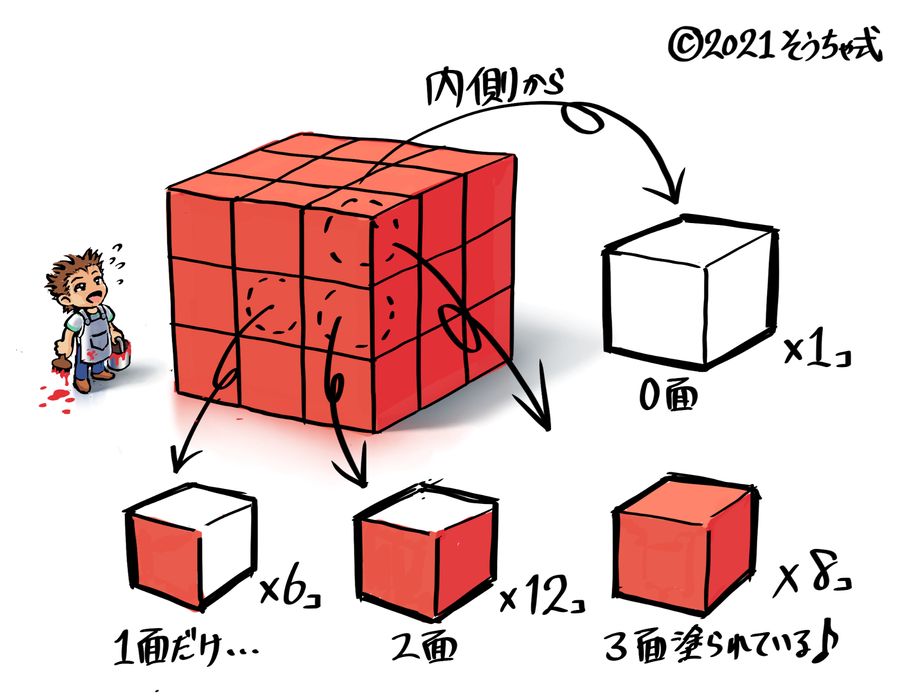
中学受験 立方体と直方体の展開図や体積表面積の求め方 公式 そうちゃ式 受験算数 2号館 図形 速さ
上記の効果は Qt 公式ルーチン Callout このルーチンの核心は、これら2つのシグナルを使用して、コントロールを動的に作成、非表示、表示することです。 レジェンドコントロールシーケンスの非表示/表示 公式ルーチンを参照する legendmarkers直方体という大きなグループの中で 全部の面が正方形によって囲まれている特別なヤツ それが立方体というモノなのです。 なので、立方体も直方体の仲間ということになります。 だから、立方体も直方体の公式と同じく (たて)×(よこ)×(高さ)公式の導き方や、体積計算の問題の解き方は、リンク先のページでご覧になれます。 お使いのブラウザでは JavaScript が無効になっています。 当サイトは数式表示に JavaScript を利用しているため、これを無効にしているとページが正しく表示されません。
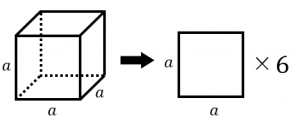
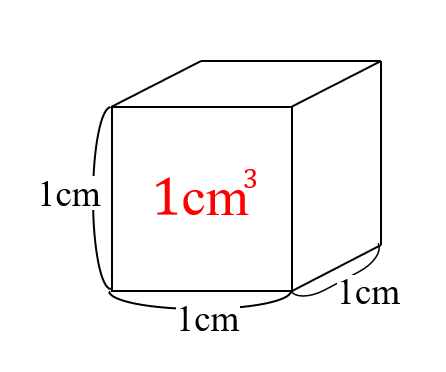
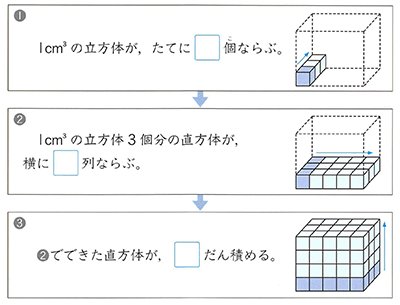
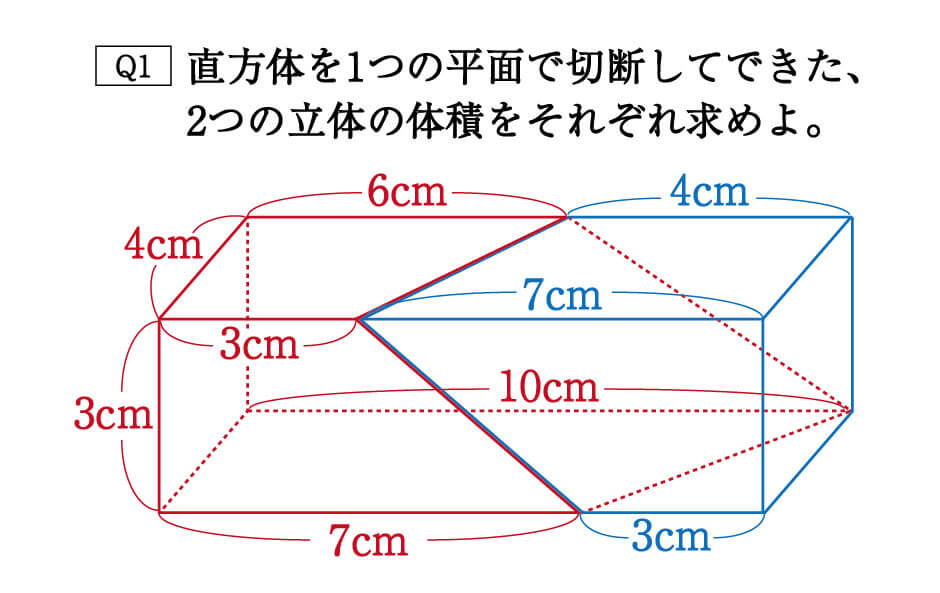
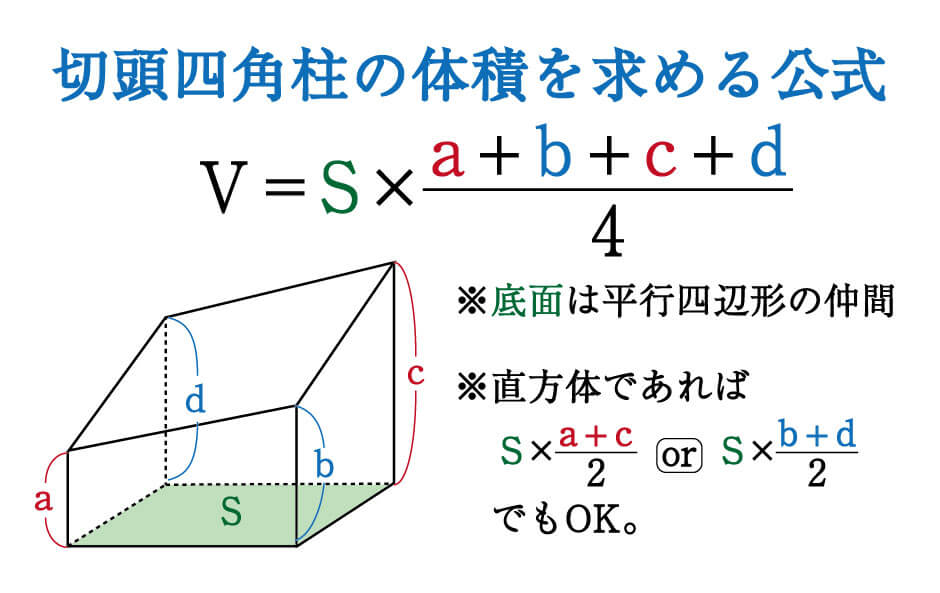
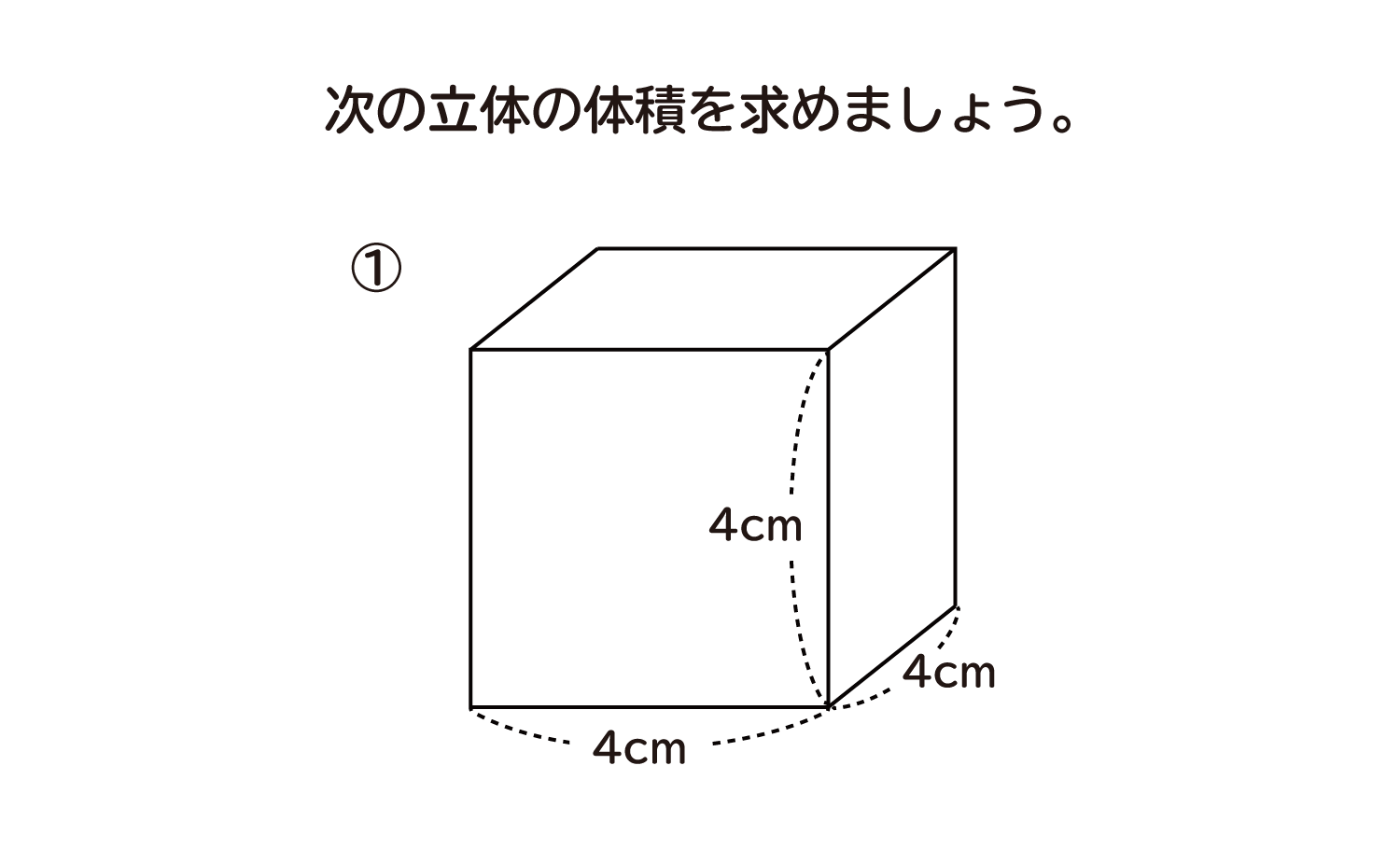
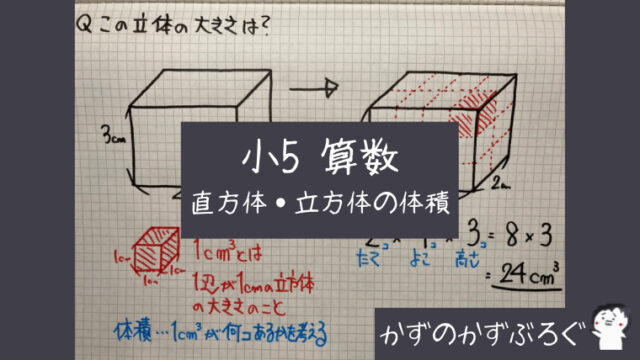
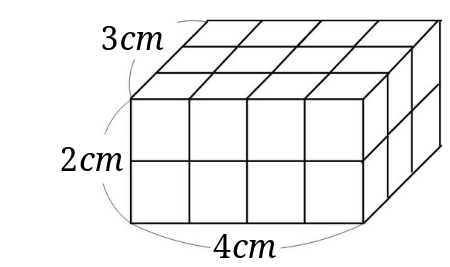
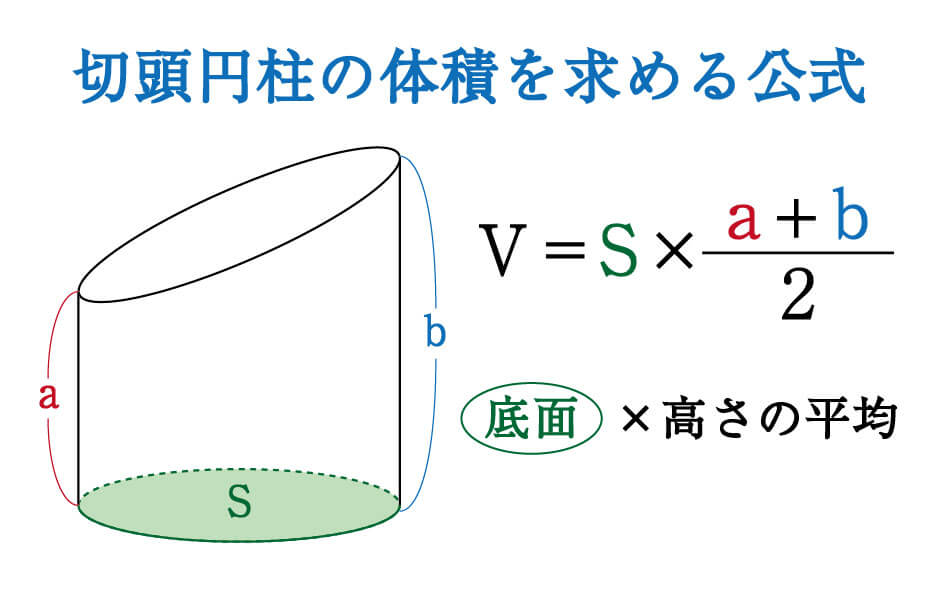
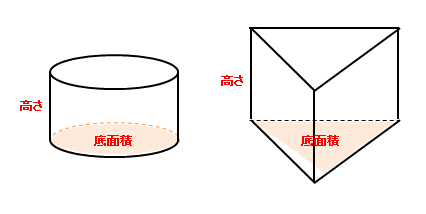
さらに立方体の辺の長さは全て同じです。縦=横=高さとなります。よって立方体の体積の公式は 辺の長さの3乗 ともいえます。 実際に下図の直方体の体積を計算してください。 立方体の公式を思い出してください。縦×横×高さでした。よって直方体や立方体の体積を計算で求める方法に気づかせ、体積を求める公式を教えます。 問題 下の直方体の体積を計算で求めましょう。 上の直方体の体積を計算で求めるには、下の図を見て下さい。 1だん目の体積を見ると、1辺が1cmの立方体が、たて3 直方体を切断したときの体積公式 直方体を切断した立体の体積は 例えば、底面をabcd、切断面をijklとおくと 底面積×(ai+bj+ck+dl)/4 で求まるわけですが、中学生向けの証明(ベクトルや重積分などを用いない) をどなたかご存じないですか?
直方体の公式のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  | |
 |  |  |
「直方体の公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「直方体の公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「直方体の公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
「直方体の公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「直方体の公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
「直方体の公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 | ||
「直方体の公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 | ||
「直方体の公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「直方体の公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「直方体の公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
「直方体の公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |
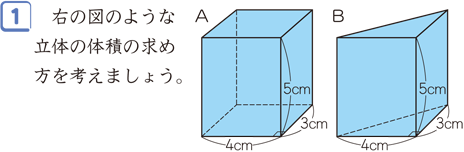
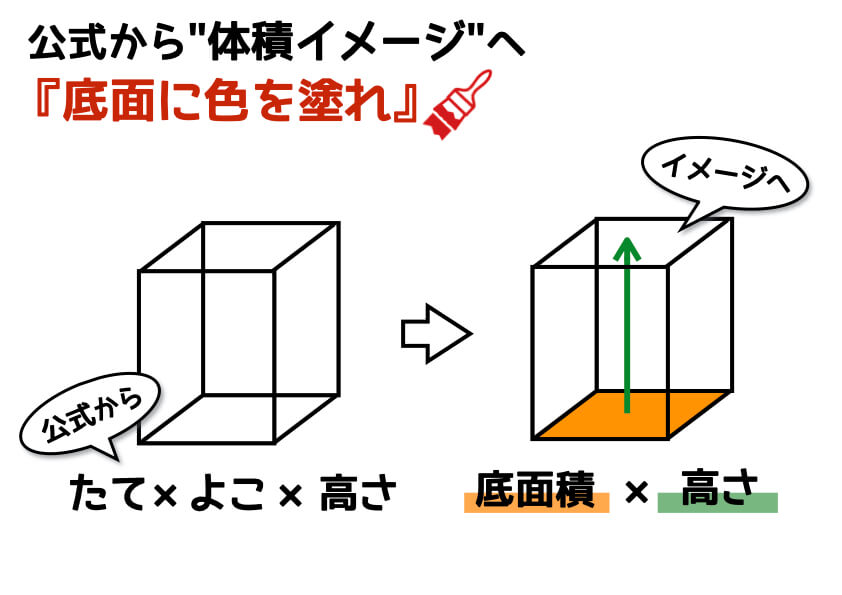
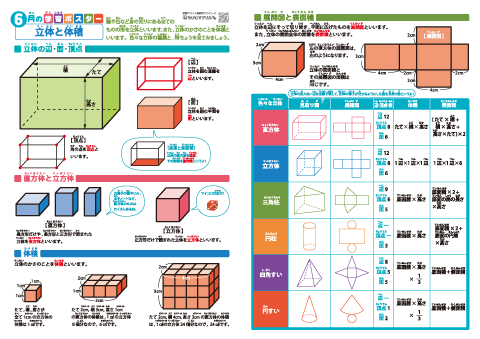
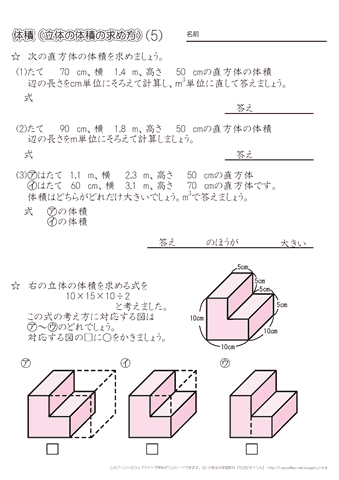
つづいて、立方体・直方体がこれらの公式で求められる理由について説明していきます。 立方体・直方体の体積が公式で求められる理由 今回2つの説明の仕方を紹介します。 説明1「長方形を積み上げる」というイメージ ・単位のちがう長さの体積を、求積公式を使って求める。 ・直方体の高さと体積の関係を説明する。 5 本時 複合図形の体積の求め方を考える。 ・複合した立体の体積の求め方を考える。 ・複合した立体を、2つの直方体の和や差ととらえる。 大 き い 体
Incoming Term: 直方体の公式,




0 件のコメント:
コメントを投稿